Dreiecke - Anwendungsaufgaben mit Abstand

Eine 5 m lange Leiter (l) wird im Abstand von 2,4 vor einer Wand aufgestellt. Wie hoch ragt die Leiter in dei Höhe ?

Erstelle eine Planskizze:

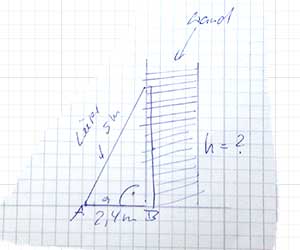
1) Bei Anwendungsaufgaben, wo mit Abstand operiert wird und senkrecht zu messnde Entfernungen im Spiel sind, sollten die Alarmglocken angehen. Meistens kann man den Satz des Pythagoras anwenden.

2) Hier ist der Satz des Pythagoras hilfreich: Gesucht wird die Höhe des rechtwinkligen Dreieicks ABS:

Es gilt: l²= h² + a²

Zahlen einsetzen ! 500 cm² = 240 cm ² + h² ⇒ h² = 500cm² - 240 cm²

⇒ h² = 250000cm² - 57600cm² ⇒ h² = 192400 cm²

Wurzel ziehen : h ≈ 438,634 cm ⇒ 4,39 m ragt die Leiter hinauf.

Kontrollmöglichkeit mit maßstabsgerechter Konstruktion nach SsW.