Dreiecke - Errechnen der Höhe oder Seiten gleichseitiger Dreiecke

In Anwendungsaufgaben kommen häufig gleichseitige Dreiecke vor, wobei entweder Höhe h oder eine Seite a bekannt ist. Es sei entweder die Höhe bekannt und a zu errechnen oder umgekehrt.

1) Berechne die Höhe eines gleichseitigen Dreiecks, wenn a = 10 cm.

2) Ein gleichseitiges Dreieck ist 80 cm hoch. Wie lang sind die Seiten ?

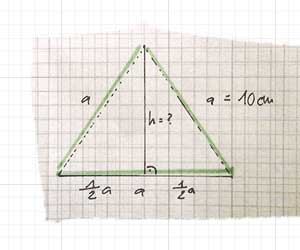
1) Wenn du eine Planskizze anfertigt, siehst du sofort, durch die Höhe besteht das gesuchte Dreieck aus zwei rechtwinkligen Teildreiecken. Der Satz des Pythagoras findet Anwendung.

2) Um a heraus zu bekommen, wenn die Höhe bekannt ist, kann man die Gleichung der ersten Aufgabe gut nutzen.

beide Seiten der Gleichung mit    dividieren!

Das Ergebnis (sinnvoll gerundet): a = 92,4 cm