Lineare Gleichungen und Ungleichungen

Die Aufgabe:

Gesucht sind alle Zahlenpaare deren Summe 4 ist

und

deren Differenz 6 ist.

Wie kann man hier vorgehen ?

Wir bezeichnen die beiden gesuchten Zahlen mit x und y. D.h. x + y = 4 und  x - y = 6

Einige Zahlenpaare, die diese Anforderungen erfüllen sind beispielsweise:

(3;1) Addition
(0;4) Addition
(8;-4) Addition: 8 + ( -4 ) = 4

(8;2) Substraktion: 8 - 2 = 6
(0;-6) Substraktion: 0 - ( -6 ) = 6
(3;-3) Substraktion: 3 - ( -3 ) = 6

Wie kann man jetzt alle Zahlenpaaren finden, welche die beiden Anforderungen erfüllen ?

Zahlenpaare, die die jeweilige Gleichung erfüllen, beschreiben wir als Lösungsmenge und schreiben dafür

L1 = {(x; y) | x+y=4}      Ʌ      L2 = {(x; y) | x-y=6}

Die beiden Gleichungen sind durch ein "und" miteinander verknüpft.

Da sich Zahlenpaare im Koordinatensystem darstellen lassen, wird man herausfinden, dass die zu L1 gehörenden Lösungen auf einer Geraden (g1) liegen und ebenfalls die Zahlenpaare von L2 liegen auf einer Geraden (g2).

Zeichnet man jetzt beide Geraden in einem Koordinatensystem, dann schneiden sich g1 und g2 in einem Punkt. Hier befindet sich die Lösung: Der Schnittpunkt liegt bei (5;-1).

Das gesuchte Zahlenpaar (5;-1) ist die Lösung.
Die Lösungsmenge dieses Systems ist L= { (5;-1) }

Es gilt L = L1 ∩ L2

Findet man die Lösungsmenge auf graphischem Wege, so nennt man das Vorgehen ein graphisches Lösen.

Ein weiteres Beispiel:

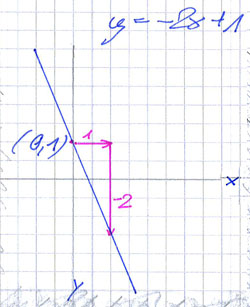
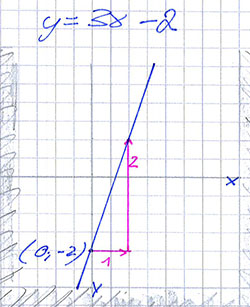
Das Lösen eines Gleichungssystems auf graphischem Weg von zwei Linearen Gleichungen in zwei Variablen ist nichts anderes als das Bestimmen des Schnittpunktes zweier Geraden.
Eine Gerade läßt sich am einfachsten zeichnen, wenn man ihre Gleichung in die
Form y = mx + b bringt.