
Drei Möglichkeiten bei Linearen Gleichungssysteme
Lineare Gleichungssysteme - Drei Möglichkeiten bei linearen Gleichungssystemen
02. Juli 2013 / Schulz
Bei Linearen Gleichungssystemen in zwei Variablen (x,y) gibt es immer drei Möglichkeiten: Wenn die Geraden, der beiden Lösungsmengen, unterschiedliche Steigungen haben, treffen sie sich logischerweise nur an einem Punkt, was bedeutet, das die Lösungsmenge 1 Element enthält.
Wenn man in einem linearen Gleichungssystem in zwei Variablen, die beiden Gleichungen nach y auflöst, so erkennt man, wie viele Zahlenpaare die Lösungen des Systems sind. y gibt Aufschluss darüber, wie viele Elemente zur Lösungsmenge gehören.
Beispiel: y = 0,8 x + 2,7 Ʌ y = 3,5 x + 9 ( Der Faktor vor dem x "beziffert" die Steigung )
Die zugehörigen Geraden haben also unterschidliche Steigungen.
Bei Linearen Gleichungssystemen in zwei Variablen (x,y) gibt es immer drei Möglichkeiten:
1.
Wenn die Geraden, der beiden Lösungsmengen, unterschiedliche Steigungen haben, treffen sie sich logischerweise nur an einem Punkt, was bedeutet, das die Lösungsmenge 1 Element enthält.
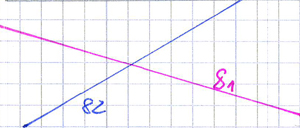
2.
Das Gleichungssystem hat keine Lösung. Das ist, wenn die beiden dazugehörigen Geraden parallel verlaufen. Logischerweise treffen sie sich dann an keinem Punkt.
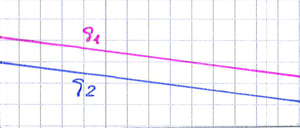
3.
Falls die zugehörigen Geraden gleich sind, gibt es unendlich viele Zahlenpaare, die zur Lösungsmenge L gehören.
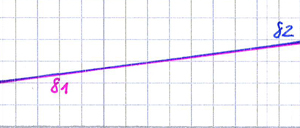
Ausbildung
- Definition der Bindungsarten Blockdrahtheftung, Spiralbindung und Wire-O-Bindung
- Was sind die Aufgaben eines Proxyservers?
- Was sind die Vor- und Nachteile einer Draht- bzw Klammerheftung?
- Symbole des Normalbruchs der unterschiedlichen Falzarten
- Was ist der Unterschied zwischen einer Blockbindung und einer Hotmelt-Technik?
BWL
- Grundbegriffe der Kosten- und Leistungsrechnung
- Zuordnung von Kosten in der Kosten- und Leistungsrechnung
- Was steckt hinter der Kostenartenrechnung?
- Einführung in die Kosten- und Leistungsrechnung
- Begriffe Aufwand und Kosten
Deutsch
- Wortbausteine
- Bindewort - Konjunktion
- Das hörbare - Dehnungs -h
- kurzgesprochene Vokale - a-e-i-o-u
- Weglassprobe
Englisch
- The plural of nouns
- The S-Genitiv
- Das Geschlecht der Nomina II
- The definite article II
- Zählbar und nicht-zählbare Begriffe
Mathe
- Wie lassen sich im Bereich der rationalen Zahlen alle Rechnungen auf Addition und Multiplikation zurückführen?
- Erkläre den Begriff Mittelsenkrechte bei einem Dreieck
- Winkelhalbierende eines Dreiecks und ihre Eigenschaften
- Dreieck - Geodreieck - Zeichengerät in der Geometrie
- Definition mathematischer Zeichen Bedeutung und Sprechweise
 alle-faecher.de
alle-faecher.de